卡塔蘭常數 
的簡單連分數表示為 [0, 1, 10, 1, 8, 1, 88, 4, 1, 1, ...] (OEIS A014538)。上方顯示了以二進位制位序列表示的連分數的前 256 項的圖。
記錄計算總結如下。
| 項 | 日期 | 作者 |
 | 2013年7月20日 | E. Weisstein |
 | 2013年8月7日 | E. Weisstein |
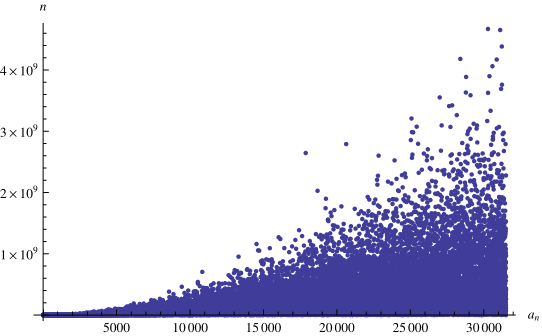
上方圖表顯示了連分數中 1、2、3、... 首次出現的位置，其中前幾個是 1、13、14、7、45、36、10、4、21、2、... (OEIS A196461；如上圖所示)。連分數的前 
項中未出現的最小數字是 31516、31591、32600、32806、33410、... (E. Weisstein，2013年8月8日)。
連分數中的累積最大項為 0、1、10、88、322、330、1102、6328、... (OEIS A099789)，它們出現在位置 0、1、2、6、105、284、747、984、2230、5377、... (OEIS A099790)。
設 
的連分數表示為 ![[a_0;a_1,a_2,...]](/images/equations/CatalansConstantContinuedFraction/Inline6.svg)
，並設收斂項的分母表示為 
、
、...、
。那麼，上面的圖表顯示了 
、
、
的連續值，它們似乎收斂於辛欽常數（左圖），以及 
，它似乎收斂於列維常數（右圖），儘管這些極限都尚未得到嚴格證明。
的 Engel 展開式由 2、2、2、4、4、5、5、12、13、41、110、... (OEIS A054543) 給出。
