楔形

術語“楔形”在數學中有許多不同的含義。

它有時被用作插入符號的另一個名稱。

該術語也指用於表示邏輯“與”的符號 ()。

在立體幾何中，像圓錐楔形、圓柱楔形和球形楔形這樣的 ungulae 通常被稱為楔形。

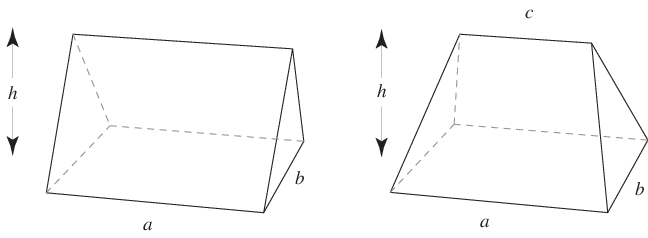
然而，當在立體幾何中單獨使用術語“楔形”時，“楔形”指的是一個直角三角形稜柱，它被旋轉使其 resting 在其一個側面矩形面上（左圖）。 Harris 和 Stocker (1998) 定義了一種更一般的斜楔形，其中頂邊對稱縮短，導致端三角形傾斜（右圖）。 從立方體中移除六個相同且方向相反的斜楔形會得到內十二面體。

對於底邊長為 和 、頂邊長為 且高為 的斜楔形（右圖），楔形的體積為

			(1)
			(2)

在直角楔形 的情況下，這簡化為

(3)

幾何質心位於高度

(4)

基底之上，對於直角楔形 ，這簡化為 的 z^_=h/3。