主題
Search

數字和

下載 Mathematica 筆記本下載 Wolfram 筆記本

數字和 s_b(n) 是基數-b 數字 n 的總和。整數 n 的以 10 為基數的數字和在 Wolfram 語言 中實現為DigitSum[n]，以及基數-b 數字和為DigitSum[n, b]。

下表給出了 s_b(n) 對於 n=1、2、... 和小 b。

bOEISs_b(n) 對於 n=1、2、...
2A0001201, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4, ...
3A0537351, 2, 1, 2, 3, 2, 3, 4, 1, 2, 3, 2, 3, 4, 3, ...
4A0537371, 2, 3, 1, 2, 3, 4, 2, 3, 4, 5, 3, 4, 5, 6, ...
5A0538241, 2, 3, 4, 1, 2, 3, 4, 5, 2, 3, 4, 5, 6, 3, ...
6A0538271, 2, 3, 4, 5, 1, 2, 3, 4, 5, 6, 2, 3, 4, 5, ...
7A0538281, 2, 3, 4, 5, 6, 1, 2, 3, 4, 5, 6, 7, 2, 3, ...
8A0538291, 2, 3, 4, 5, 6, 7, 1, 2, 3, 4, 5, 6, 7, 8, ...
9A0538301, 2, 3, 4, 5, 6, 7, 8, 1, 2, 3, 4, 5, 6, 7, ...
10A0079531, 2, 3, 4, 5, 6, 7, 8, 9, 1, 2, 3, 4, 5, 6, ...
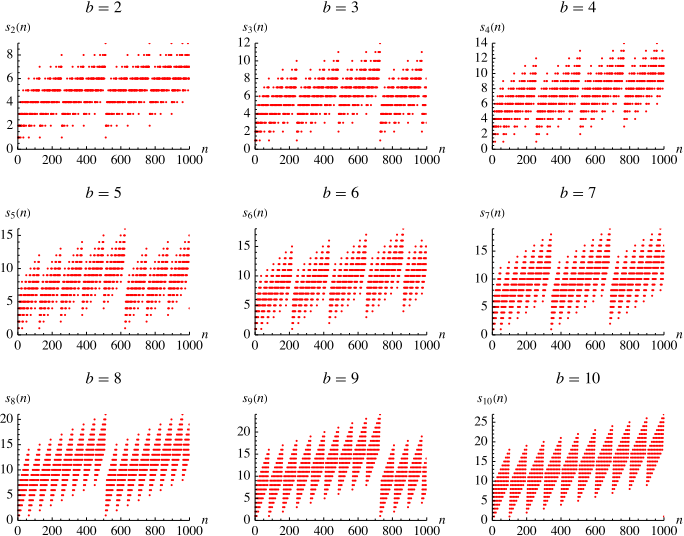
DigitSums

上面展示了前一千個正整數的數字和在基數 2 到 10 時的圖。

DigitSum

繪製 s_b(n) 與 b 和 n 的關係圖，得到如上所示的圖。

數字和 s_b(n) 滿足同餘式

n=s_b(n) (mod b-1).
(1)

在以 10 為基數的情況下，這個同餘式是 棄九法 和快速 整除性檢驗（例如 3 和 9 的整除性檢驗）的基礎。

s_b(n) 滿足以下令人意外的恆等式

sum_(n=1)^infty(s_b(n))/(n(n+1))=b/(b-1)lnb,
(2)

其中 b=2 的情況在 1981 年普特南競賽中給出 (Allouche 1992)。 此外，

sum_(n=1)^(infty)s_2(n)(2n+1)/(n^2(n+1)^2)=(pi^2)/9
(3)
sum_(n=2)^(infty)[s_2(n)]^2(8n^3+4n^2+n-1)/(4n(n^2-1)(4n^2-1))=(17)/(24)+ln2
(4)

(OEIS A100044 和 A100045; Allouche 1992, Allouche 和 Shallit 1992)。

設 u(n) 為 數字塊 11 在 n 的二進位制展開式中的數量，則

sum_(n=1)^(infty)(u(n))/(n(n+1))=3/2ln2-1/4pi
(5)

(OEIS A100046; Allouche 1992)。

Sondow (2006) 指出了令人意外的恆等式

product_(n=0)^inftyproduct_(k=1,3,...)^(b-1)((nb+k)/(nb+k+1))^((-1)^(s_b(n)))=1/(sqrt(b)).
(6)

b=2 的特殊情況對應於 Thue-Morse 序列 乘積 (J. Sondow，私人通訊，2006 年 10 月 31 日)。

數字 1、81、1458 和 1729 (OEIS A110921) 都是它們自身數字和及其反轉的乘積，例如 1+7+2+9=19，以及 19×91=1729。 藤原 (Fujiwara 和 Ogawa 2005) 證明了只有這四個數字具有此屬性。

另請參閱

棄九法, 數字根, 數字, 數字塊, 數字計數, 數字乘積, 整除性檢驗

相關的 Wolfram 站點

http://functions.wolfram.com/NumberTheoryFunctions/DigitCount/

此條目的部分內容由 Topher Cooper 貢獻

使用 探索

參考文獻

Allouche, J.-P. "Series and Infinite Products Related to Binary Expansions of Integers." 1992. http://algo.inria.fr/seminars/sem92-93/allouche.ps.Allouche, J.-P. and Shallit, J. "The Ring of k-Regular Sequences." Theor. Comput. Sci. 98, 163-197, 1992.Fujiwara, M. and Ogawa, Y. Introduction to Truly Beautiful Mathematics. Tokyo: Chikuma Shobo, 2005.Grabner, P. J.; Herendi, T.; and Tichy, R. F. "Fractal Digital Sums and Codes." Appl. Algebra Engrg. Comm. Comput. 8, 33-39, 1997.Shallit, J. O. "On Infinite Products Associated with Sums of Digits." J. Number Th. 21, 128-134, 1985.Sloane, N. J. A. Sequences A000120/M0105, A007953, A053735, A053737, A053824, A053827, A053828, A053829, A053830, A100044, A100045, and A100046 in "The On-Line Encyclopedia of Integer Sequences."Sondow, J. "Problem 11222." Amer. Math. Monthly 113, 459, 2006.Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, p. 218, 2004. http://www.mathematicaguidebooks.org/.

在 中被引用

數字和

請引用為

Cooper, Topher 和 Weisstein, Eric W. “數字和。” 來自 —— 資源。 https://mathworld.tw/DigitSum.html

主題分類