Moser (1966) 提出了以下問題:在單位寬度的二維走廊中,面積最大的平面圖形(“沙發”) 能夠繞過直角拐角移動。一個面積為
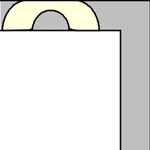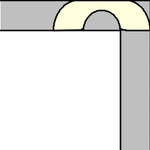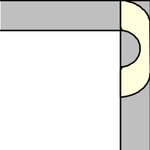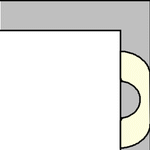
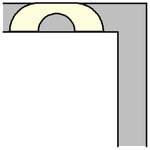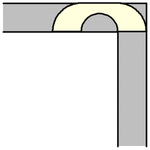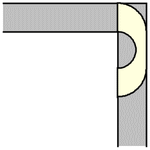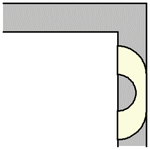
能夠繞過直角拐角移動。一個面積為  的單位正方形 可以很容易地“繞過”拐角移動,只需沿著走廊推動它直到碰到遠處的牆壁,然後沿著垂直的走廊拉動它即可,如上圖所示(Rommik 2016)。
的單位正方形 可以很容易地“繞過”拐角移動,只需沿著走廊推動它直到碰到遠處的牆壁,然後沿著垂直的走廊拉動它即可,如上圖所示(Rommik 2016)。
雖然單位正方形可以在不旋轉的情況下“繞過”拐角移動,但當允許旋轉時,移動更大的形狀是可能的。要考慮的最簡單的這種形狀是半單位圓盤(填充的半圓),其面積為  ,它可以像上圖所示那樣滑過拐角(Rommik 2016)。
,它可以像上圖所示那樣滑過拐角(Rommik 2016)。
Hammersley(Croft等人1994,Rommik)透過將半圓盤切割成兩個四分之一圓盤進一步增加了面積,將它們水平分隔開  的距離,同時填充它們之間的間隙。此外,他從底部移除了一個半徑為
的距離,同時填充它們之間的間隙。此外,他從底部移除了一個半徑為  的較小半圓盤,從而產生了一個可以稱為 Hammersley 沙發 的形狀。當
的較小半圓盤,從而產生了一個可以稱為 Hammersley 沙發 的形狀。當  時,其面積最大化,得到面積
時,其面積最大化,得到面積
(OEIS A086118;Croft等人1994,Rommik)。事實證明,對於任何值  ,包括給出最大面積的半徑
,包括給出最大面積的半徑  ,Hammersley 沙發都可以繞過拐角移動。最大 Hammersley 沙發繞過拐角的過程如上圖所示(Romik 2016)。
,Hammersley 沙發都可以繞過拐角移動。最大 Hammersley 沙發繞過拐角的過程如上圖所示(Romik 2016)。
Gerver (1992) 發現了一種面積為 2.219531...(OEIS A128463;這個數字可以稱為 移動沙發常數)的沙發,略大於 Hammersley 最優沙發的面積 2.207416...(OEIS A086118)。這種沙發可以繞過拐角移動,Gerver (1992) 提供的論證表明它要麼是最優的,要麼接近最優。Gerver 沙發的邊界是一個複雜的形狀,由 3 條直線段和 15 個曲線段組成,每個曲線段都由解析表示式描述。Gerver 沙發繞過轉角的動畫如上圖所示(Romik 2016)。
假設軌跡和包絡線是凸的,Deng (2024) 使用變分法在一組曲線的引數方程上構建了一個積分泛函,透過求解尤拉-拉格朗日微分方程來確定沙發形狀。使用數值方法,這給出了一個面積為 2.2195316 的形狀,與 Gerver 沙發一致。Baek (2024) 證明了 Gerver 的構造達到了最大面積 2.2195...,其證明不需要計算機輔助,只需使用科學計算器進行數值計算即可。
另請參閱
Gerver 沙發,
Hammersley 沙發,
移動沙發常數,
鋼琴搬運工問題
使用 探索
參考文獻
Baek, J. "Gerver 沙發的最優性。" 2024 年 11 月 29 日。https://arxiv.org/abs/2411.19826。Croft, H. T.; Falconer, K. J.; 和 Guy, R. K. 幾何學中的未解決問題。 紐約:Springer-Verlag,1994 年。Deng, Z. "移動沙發問題的變分法方法和尤拉-拉格朗日方程。" 2024 年 8 月。 https://community.wolfram.com/groups/-/m/t/3234695。Deng, Z. "使用變分法解決移動沙發問題。" 2024 年 7 月 2 日。 https://arxiv.org/abs/2407.02587。Finch, S. R. "移動沙發常數。" 數學常數。 第 8.12 節。英國劍橋:劍橋大學出版社,第 519-523 頁,2003 年。Gerver, J. L. "關於移動沙發繞過拐角。" Geometriae Dedicata 42, 267-283, 1992.Kallus, Y. 和 Romik, D. "移動沙發問題中改進的上限。" Adv. in Math. 340, 960-982, 2018.Moser, L. "問題 66Ð11:在走廊中移動傢俱。" SIAM Rev. 8, 381, 1966.Romik, D. "MovingSofas:論文“移動沙發問題中的微分方程和精確解”的配套 Mathematica 包。" 包版本:1.3。2016 年 7 月 10 日。 https://www.math.ucdavis.edu/~romik/data/uploads/software/movingsofas-v1.3.nb。Romik, D. "移動沙發問題中的微分方程和精確解。" Exper. Math. 27, 316-330, 2018.Romik, D. "Dan Romik 的主頁:移動沙發問題。" https://www.math.ucdavis.edu/~romik/movingsofa/。Sloane, N. J. A. 序列 A086118 和 A128463,來自“整數序列線上百科全書”。Stewart, I. 你又讓我陷入了精妙的數學.... 紐約:W. H. Freeman,1992 年。Trott, M. Mathematica 程式設計指南。 紐約:Springer-Verlag,第 104 頁,2004 年。 http://www.mathematicaguidebooks.org/。在 中被引用
移動沙發問題
請引用為
Weisstein, Eric W. “移動沙發問題。” 來自 -- Wolfram 網路資源。 https://mathworld.tw/MovingSofaProblem.html
主題分類
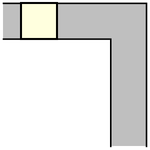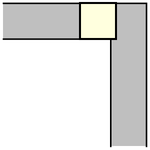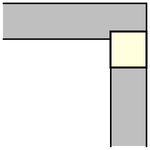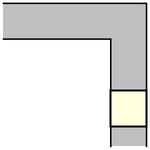
能夠繞過直角拐角移動。一個面積為
的單位正方形 可以很容易地“繞過”拐角移動,只需沿著走廊推動它直到碰到遠處的牆壁,然後沿著垂直的走廊拉動它即可,如上圖所示(Rommik 2016)。
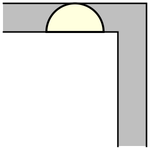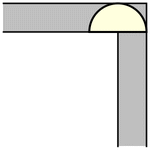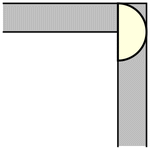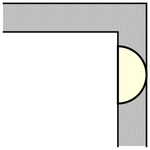
,它可以像上圖所示那樣滑過拐角(Rommik 2016)。
的距離,同時填充它們之間的間隙。此外,他從底部移除了一個半徑為
的較小半圓盤,從而產生了一個可以稱為 Hammersley 沙發 的形狀。當
時,其面積最大化,得到面積
,包括給出最大面積的半徑
,Hammersley 沙發都可以繞過拐角移動。最大 Hammersley 沙發繞過拐角的過程如上圖所示(Romik 2016)。