Hammersley 沙發

在移動沙發問題中，即尋找最大面積 的平面圖形（“沙發”），使其能夠在一個單位寬度的二維走廊的直角轉角處移動，Hammersley（Croft et al. 1994, Rommik）發現了一種形狀，其面積大於半圓盤，方法是將半圓盤切割成兩個四分之一圓盤，水平分隔一段距離 ，同時填充它們之間的間隙。此外，從底部移除了一個半徑為 的較小半圓盤，如上圖所示。

所得的“Hammersley 沙發”如上圖所示，針對不同的 值，形狀從 時的半圓盤變為 時兩半在單點相遇的形狀。

Hammersley 沙發的面積

(1)

和周長

(2)

正如預期的那樣，當 時，面積和周長會減小到半圓盤 和 的值。上面顯示了 作為 從 到 的函式圖。

當 最大化時，，得到面積

(3)

（OEIS A086118； Croft et al. 1994, Rommik）。

最大 Hammersley 沙發如上圖所示。

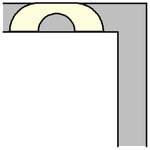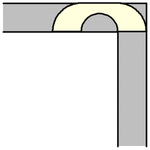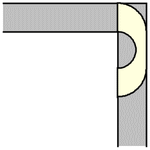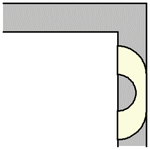
事實證明，對於任何值 ，包括給出最大面積的半徑 ，Hammersley 沙發都可以繞過角落。上面展示了最大 Hammersley 沙發繞過角落的過程 (Romik 2016)。

後來發現了一種稍大的沙發，現在稱為Gerver 沙發，並最終被證明是最佳的。