由下式定義的一般四次曲面
 |
(1)
|
(Gray 1997, 第 314 頁)。 上面兩幅影像分別對應於  , 和
, 和  , 分別地。
, 分別地。
上面展示了其他情況。
對應於  的“圓角立方體”情況是體積為 超橢球體
的“圓角立方體”情況是體積為 超橢球體
 |
(2)
|
其中  是 伽瑪函式。
是 伽瑪函式。
情況  的體積由下式給出
的體積由下式給出
其中
 |
(5)
|
![R[z]](/images/equations/GoursatsSurface/Inline12.svg) 是
是  的實部,而
的實部,而  是第一類貝塞爾函式 (E. W. Weisstein 和 M. Trott,私人通訊,2008 年 11 月 9 日),這可能可以用二元超幾何函式以閉合形式表示。
是第一類貝塞爾函式 (E. W. Weisstein 和 M. Trott,私人通訊,2008 年 11 月 9 日),這可能可以用二元超幾何函式以閉合形式表示。
相關的曲面
 |
(6)
|
對於  的偶數整數,Gray(1997,第 292 頁)也考慮了這種情況,它是超橢球體的一個特例。
的偶數整數,Gray(1997,第 292 頁)也考慮了這種情況,它是超橢球體的一個特例。
另請參閱
Chmutov 曲面,
立方體,
超橢球體,
齒狀曲面
使用 探索
參考文獻
Banchoff, T. F. "Computer Graphics Tools for Rendering Algebraic Surfaces and for Geometry of Order." In Geometric Analysis and Computer Graphics: Proceedings of a Workshop Held May 23-25, 1988 (Eds. P. Concus, R. Finn, D. A. Hoffman). New York: Springer-Verlag, pp. 31-37, 1991.Goursat, E. "Étude des surfaces qui admettent tous les plans de symétrie d'un polyèdre régulier." Ann. Sci. École Norm. Sup. 4, 159-2000, 1897.Gray, A. Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, pp. 292 and 314, 1997.
請引用為
Weisstein, Eric W. “Goursat 曲面。” 來自 Web 資源。 https://mathworld.tw/GoursatsSurface.html
主題分類
, 和
, 分別地。
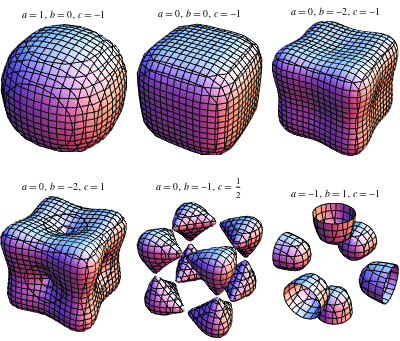
的“圓角立方體”情況是體積為 超橢球體

是 伽瑪函式。
的體積由下式給出

![int_0^infty-(pi^2)/(16sqrt(2))R{((-1)^(5/8))/(t^(7/4))[(-1)^(1/4)e^(it/8)t^(3/4)×[(-1)^(3/4)J_(1/4)(t/8)-J_(-1/4)(t/8)]^3+(12sqrt(t)Gamma(1/4))/(pi^2)+(2(1+i)Gamma^3(1/4))/(pi^3)]}dt](/images/equations/GoursatsSurface/Inline11.svg)
是
的實部,而
是第一類貝塞爾函式 (E. W. Weisstein 和 M. Trott,私人通訊,2008 年 11 月 9 日),這可能可以用二元超幾何函式以閉合形式表示。
的偶數整數,Gray(1997,第 292 頁)也考慮了這種情況,它是超橢球體的一個特例。