主題
Search

菲涅耳積分

下載 Mathematica 筆記本下載 Wolfram 筆記本
Fresnel

菲涅耳積分的定義略有不同。在物理學中，菲涅耳積分用 C(u) 和 S(u) 表示，最常見的定義為

C(u)+iS(u)=int_0^ue^(ipix^2/2)dx
(1)
=int_0^ucos(1/2pix^2)dx+iint_0^usin(1/2pix^2)dx,
(2)

所以

C(u)=int_0^ucos(1/2pix^2)dx
(3)
S(u)=int_0^usin(1/2pix^2)dx.
(4)

這些菲涅耳積分在 Wolfram 語言 中實現為FresnelC[z] 和FresnelS[z]。

C(u) 和 S(u) 是 整函式。

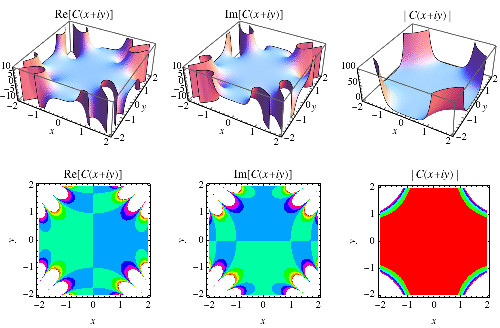FresnelCReImAbs
最小值 最大值
實部
虛部 Powered by webMathematica
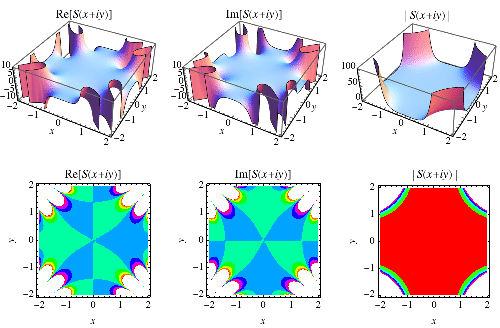FresnelSReImAbs
最小值 最大值
實部
虛部 Powered by webMathematica

C(u) 和 S(u) 積分在複平面上如上所示。

它們具有特殊值

C(-infty)=-1/2
(5)
C(0)=0
(6)
C(infty)=1/2
(7)

和

S(-infty)=-1/2
(8)
S(0)=0
(9)
S(infty)=1/2.
(10)

u>>1 的漸近展開式給出

C(u) approx 1/2+1/(piu)sin(1/2piu^2)
(11)
S(u) approx 1/2-1/(piu)cos(1/2piu^2).
(12)

因此，當 u->infty 時，C(u)=1/2 且 S(u)=1/2。菲涅耳積分有時也另定義為

x(t)=int_0^tcos(v^2)dv
(13)
y(t)=int_0^tsin(v^2)dv.
(14)

令 x=v^2，則 dx=2vdv=2sqrt(x)dv，且 dv=x^(-1/2)dx/2

x(t)=1/2int_0^(sqrt(t))x^(-1/2)cosxdx
(15)
y(t)=1/2int_0^(sqrt(t))x^(-1/2)sinxdx.
(16)

在這種形式下，它們在 第一類球貝塞爾函式 方面具有特別簡單的展開式。使用

j_0(x)=(sinx)/x
(17)
n_1(x)=-j_(-1)(x)
(18)
=-(cosx)/x,
(19)

其中 n_1(x) 是 第二類球貝塞爾函式

x(t^2)=-1/2int_0^tn_1(x)x^(1/2)dx
(20)
=1/2int_0^tj_(-1)(x)x^(1/2)dx
(21)
=x^(1/2)sum_(n=0)^(infty)j_(2n)(x)
(22)
y(t^2)=1/2int_0^tj_0(x)x^(1/2)dx
(23)
=x^(1/2)sum_(n=0)^(infty)j_(2n+1)(x).
(24)

相關函式 C_1(z)、C_2(z)、S_1(z) 和 S_2(z) 定義為

C_1(z)=C(sqrt(2/pi)z)=sqrt(2/pi)int_0^zcost^2dt
(25)
S_1(z)=S(sqrt(2/pi)z)=sqrt(2/pi)int_0^zsint^2dt
(26)
C_2(z)=C(sqrt((2z)/pi))=1/(sqrt(2pi))int_0^z(cost)/(sqrt(t))dt
(27)
S_2(z)=S(sqrt((2z)/pi))=1/(sqrt(2pi))int_0^z(sint)/(sqrt(t))dt.
(28)

另請參閱

科爾努螺線

相關 Wolfram 網站

http://functions.wolfram.com/GammaBetaErf/FresnelC/, http://functions.wolfram.com/GammaBetaErf/FresnelS/

透過 探索

參考文獻

Abramowitz, M. 和 Stegun, I. A. (Eds.). "菲涅耳積分。" §7.3 in 數學函式手冊，包含公式、圖表和數學表格，第 9 次印刷。 New York: Dover, pp. 300-302, 1972.Leonard, I. E. "關於菲涅耳積分的更多內容。" Amer. Math. Monthly 95, 431-433, 1988.Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; 和 Vetterling, W. T. "菲涅耳積分、餘弦積分和正弦積分。" §6.79 in FORTRAN 數值食譜：科學計算的藝術，第 2 版。 Cambridge, England: Cambridge University Press, pp. 248-252, 1992.Prudnikov, A. P.; Marichev, O. I.; 和 Brychkov, Yu. A. "廣義菲涅耳積分 S(x,nu) 和 C(x,nu)。" §1.3 in 積分與級數，卷 3：更多特殊函式。 Newark, NJ: Gordon and Breach, p. 24, 1990.Spanier, J. 和 Oldham, K. B. "菲涅耳積分 S(x) 和 C(x)。" Ch. 39 in 函式圖譜。 Washington, DC: Hemisphere, pp. 373-383, 1987.

在 上被引用

菲涅耳積分

引用為

Weisstein, Eric W. "菲涅耳積分。" 來自 網路資源。 https://mathworld.tw/FresnelIntegrals.html

學科分類