橢圓指數函式 給出了 橢圓對數 中
的值
對於 和
為實數,使得
。
它在 Wolfram 語言 中實現為EllipticExp[u, a, b
],它返回
以及多餘的引數
,該引數將上述積分乘以因子
。
上面的頂部圖顯示了 (紅色),
(紫色), 和
(藍色),對於
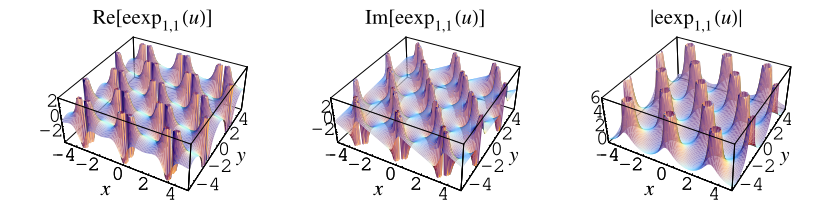
。其他圖顯示了 複平面 中的
。
上面的圖顯示了 複平面 中對於 的
。
橢圓指數函式 給出了 橢圓對數 中
的值
對於 和
為實數,使得
。
它在 Wolfram 語言 中實現為EllipticExp[u, a, b
],它返回
以及多餘的引數
,該引數將上述積分乘以因子
。

上面的頂部圖顯示了 (紅色),
(紫色), 和
(藍色),對於
。其他圖顯示了 複平面 中的
。
上面的圖顯示了 複平面 中對於 的
。
Weisstein, Eric W. "橢圓指數函式。" 來自 —— 資源。 https://mathworld.tw/EllipticExponentialFunction.html