橢圓對數

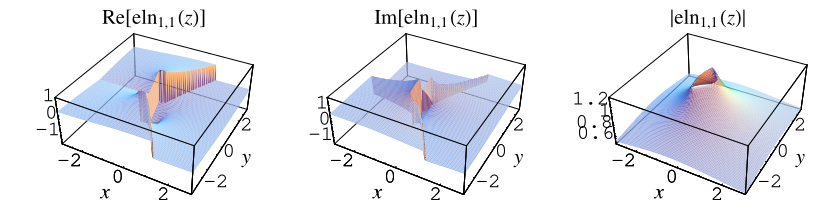
橢圓對數是如下形式積分的推廣的形狀

對於 實數，它可以表示為對數和反三角函式，到

對於 和 實數。這個積分可以解析地完成，但是具有複雜的形狀，涉及到具有復引數的第一類不完全橢圓積分。上面的圖顯示了特殊情況 。

橢圓對數在 Wolfram 語言 中實現為EllipticLog[x, y, a, b], 其中 是一個不幸且多餘的引數，必須設定為 或 ，並將上述積分乘以一個因子 。

橢圓對數的逆是橢圓指數函式。