圓柱-圓柱 相交

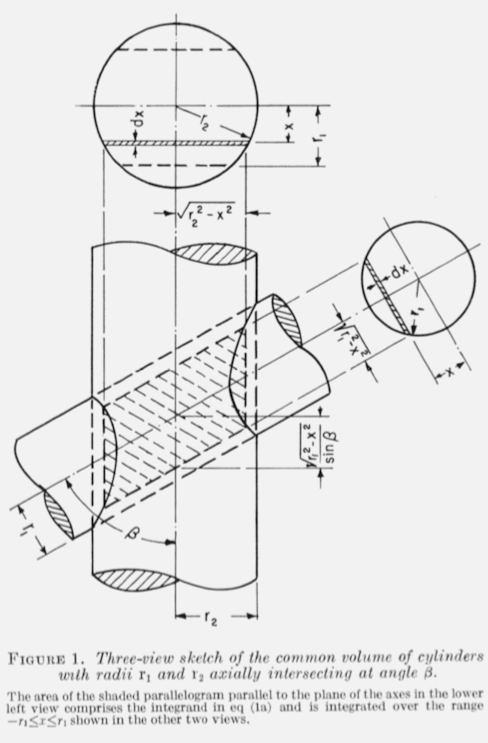
考慮如上圖所示的兩個圓柱體（Hubbell 1965），其中圓柱體的半徑為 和 ，且 ，較大的圓柱體沿 -軸方向，並且兩個圓柱體的軸線以角度 相交。那麼相交區域的體積由下式給出

			(1)
			(2)
			(3)
			(4)
			(5)

其中

(6)

這裡， 和 分別是第一類和第二類完全橢圓積分， 是一個超幾何函式，而 是一個二項式係數。

兩個（或三個）半徑相等的直圓柱以直角相交的交集被稱為施泰因梅茨體。