協同學座標

協同學座標是在其平面上的一組三角形座標（或它們在空間中的四面體座標的推廣，或更高維度中的類似物）。在平面中，座標 沿三個軸 、 和 測量，其中 -軸向下定向， 軸和 軸彼此之間以 度角定向，如上圖所示（左圖）。將 、 和 解釋為透過從原點平行位移三對彼此之間以 度角定向的線而獲得的等邊三角形邊上的點，座標 可以解釋為指定給定的等邊三角形（右圖）。

這些座標的一個很好的性質是，透過 平行位移獲得的三角形的頂點由 、 和 給出（見上圖），因此頂點座標的總和始終為零。當座標推廣到三維和更高維度時，此屬性也成立。

協同學座標還具有以下性質：由 描述的等邊三角形的邊長恰好是 ，這同樣可以推廣到更高維度。

協同學座標為構建規則的圓形和球形堆積提供了一種便捷的方法。例如，左上方所示的圓環可以透過選擇所有整數協同學座標 集來生成，這些座標的總和為零，並且三個座標的絕對值之和除以二等於一 (Nelson)。類似地，第二個圓環可以從所有整數座標集中獲得，這些座標的總和為零，並且三個座標的絕對值之和除以二等於一。零環、第一環和第二環如右上方所示。

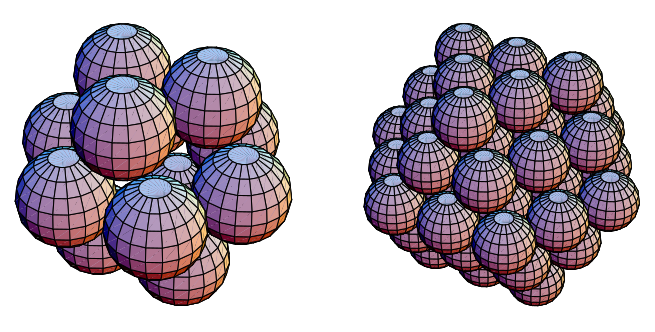
類似的性質在三維中也成立，其中適當的協同學座標 集在規則球體堆積中給出連續的殼層 (Nelson)，如上圖所示。