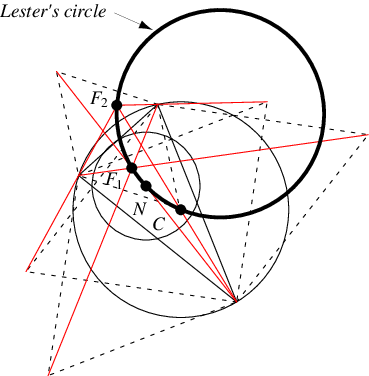
萊斯特圓是外心 
、九點圓圓心 
以及第一和第二費馬點 
和 
所在的圓（Kimberling 1998，第 229-230 頁）。除了這些（金伯林中心 
、
、
和 
，分別為），沒有其他著名的三角形中心位於該圓上。
萊斯特圓具有圓函式
![l=-(f(a,b,c)R^2[1+2cos(2A)])/(6a^2bc(a^2-b^2)(a^2-c^2)),](/images/equations/LesterCircle/NumberedEquation1.svg) |
(1)
|
其中
 |
(2)
|
似乎沒有簡單的形式，並且 
沒有出現在 Kimberling 的三角形中心列表中。萊斯特圓的圓心是
![alpha=bc(b^2-c^2)[2(a^2-b^2)(c^2-a^2)+3R^2(2a^2-b^2-c^2)-a^2(a^2+b^2+c^2)+a^4+b^4+c^4],](/images/equations/LesterCircle/NumberedEquation3.svg) |
(3)
|
其中 
是參考三角形的外接圓半徑，即金伯林中心 
。萊斯特圓的半徑由下式給出
 |
(4)
|
其中 
是一個 16 階對稱多項式，似乎沒有簡單的形式。
它與垂心-重心圓正交。
Trott, M. "萊斯特圓定理的證明。"