在組合邏輯最小化中,一種稱為卡諾圖的工具經常被使用。它類似於真值表,但是不同的變數沿著兩個軸表示,並且以這樣的方式排列:從一個方格移動到相鄰方格時,只有一個輸入位發生變化。它也被稱為 Veitch 圖、K 圖或 KV 圖。
卡諾圖可用於快速消除布林函式中的冗餘操作。最容易閱讀的卡諾圖是為完全積或“積之和”形式的函式繪製的圖,其中後一個名稱也暗示了 AND 和 OR 運算子的使用。在這種函式的典型真值表中,輸入使用 0 表示假,1 表示真來列舉,並在作為正二進位制整數讀取時按計數序列排序。下面說明了四個變數的函式的真值表。
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 1 | 0 | |
| 0 | 0 | 1 | 0 | 1 | |
| 0 | 0 | 1 | 1 | 1 | |
| 0 | 1 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 1 | 0 | |
| 0 | 1 | 1 | 0 | 1 | |
| 0 | 1 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | 1 | |
| 1 | 0 | 0 | 1 | 0 | |
| 1 | 0 | 1 | 0 | 0 | |
| 1 | 0 | 1 | 1 | 0 | |
| 1 | 1 | 0 | 0 | 1 | |
| 1 | 1 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 0 | 0 | |
| 1 | 1 | 1 | 1 | 0 |
對於表中函式值為 1(真)的行,顯示了一個稱為最小項的邏輯表示式。最小項使用上劃線符號表示 NOT。當所有七個最小項累積時,
|
(1)
|
該函式得以實現。這種實現不是最優的,可以使用卡諾圖來簡化它。
上面顯示了該函式的卡諾圖。它是真值表的二維佈局。每個維度跨越一對相鄰的(但不一定是如此的)變數。變數的序列不是計數序列,而是格雷碼,因此在每對相鄰單元格(在行或列中)之間,只有一個變數改變狀態。
在地圖上,函式值為 1 的相鄰單元格用環分組在一起。每個環代表可以簡化的最小項。環內變化的變數可以被消除。使用最上面的表示式作為示例,可以代數地證明其有效性。
|
(2)
| |||
|
(3)
| |||
|
(4)
|
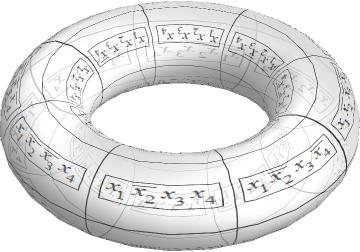
環也可以繪製成環繞行和/或列,因為卡諾圖(最多四個變數)實際上是環面的表面。
類似於上面示例的卡諾圖也可以類似地為兩個(退化)或三個變數繪製。它們可以用於超過四個變數(例如,透過疊加兩個四變數圖來處理五個變數),但是視覺化變得比代數更繁瑣。