Hénon-Heiles 方程是一個非線性不可積的 哈密頓系統,其具有
其中勢能函式由極座標方程定義
 |
(3)
|
給出笛卡爾勢
 |
(4)
|
系統的總能量由下式給出
 |
(5)
|
在運動過程中是守恆的。
從任意起點積分上述耦合常微分方程,初始條件為  和
和  ,得到如上所示的運動。
,得到如上所示的運動。
上面展示了不同初始能量  下的截面,在
下的截面,在  相對於
相對於  的圖,在
的圖,在  的值處。
的值處。
廣義 Hénon-Heiles 勢的哈密頓量是
 |
(6)
|
運動方程僅在以下情況下可積
1.  ,
,
2.  ,
,
3.  ,以及
,以及
4.  .
.
上面的圖顯示了具有廣義 Hénon-Heiles 勢的薛定諤方程的一些本徵函式
 |
(7)
|
對於  的某些特定值 (M. Trott, 私人通訊, 2004年1月6日)。
的某些特定值 (M. Trott, 私人通訊, 2004年1月6日)。
另請參閱
標準對映,
截面
使用 探索
參考文獻
Gleick, J. Chaos: Making a New Science. New York: Penguin Books, pp. 144-153, 1988.Hénon, M. and Heiles, C. "The Applicability of the Third Integral of Motion: Some Numerical Experiments." Astron. J. 69, 73-79, 1964.Rasband, S. N. Chaotic Dynamics of Nonlinear Systems. New York: Wiley, pp. 171-172, 1990.Tabor, M. "The Hénon-Heiles Hamiltonian." §4.1.b in Chaos and Integrability in Nonlinear Dynamics: An Introduction. New York: Wiley, pp. 121-122, 1989.Trott, M. "The Mathematica Guidebooks Additional Material: Hénon-Heiles Eigenfunctions." http://www.mathematicaguidebooks.org/additions.shtml#S_2_01.在 中被引用
Hénon-Heiles 方程
請引用為
Weisstein, Eric W. "Hénon-Heiles 方程。" 來自 Web 資源。 https://mathworld.tw/Henon-HeilesEquation.html
主題分類
和
,得到如上所示的運動。
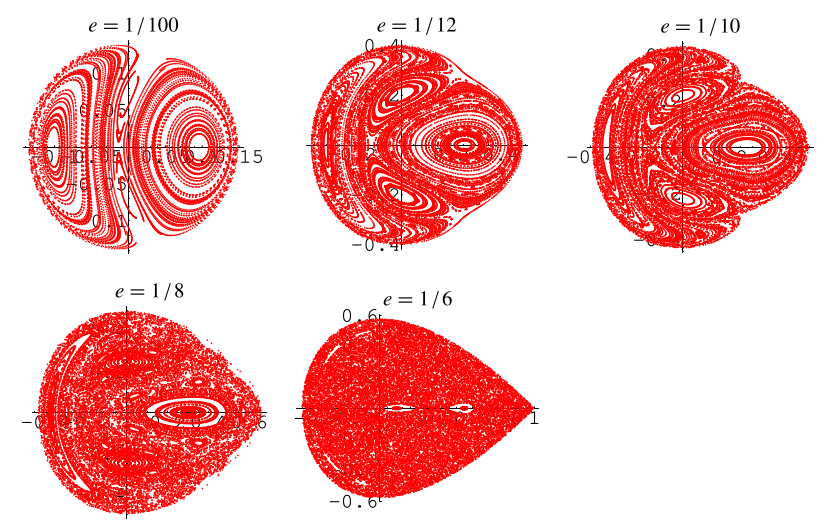
下的截面,在
相對於
的圖,在
的值處。
,
,
,以及
.
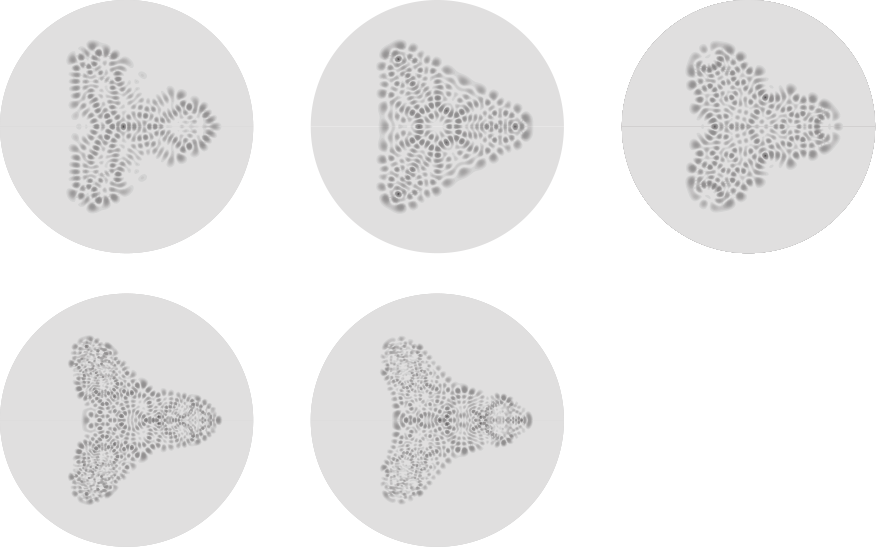
的某些特定值 (M. Trott, 私人通訊, 2004年1月6日)。