主題
Search

清潔瓷磚問題

DOWNLOAD Mathematica Notebook下載 Wolfram 筆記本

清潔瓷磚是一個由布豐 (Buffon) (1777 年) 研究的遊戲，玩家在規則鋪砌的地板上投擲硬幣，並投注硬幣將部分覆蓋的不同瓷磚的數量。布豐研究了三角網格、正方網格、六邊形網格和由菱形組成的網格上的機率。假設瓷磚的邊長 l 大於硬幣直徑 d。那麼，在正方網格上，硬幣可能以某種方式落下，使得它部分覆蓋 1、2、3 或 4 塊瓷磚。在三角網格上，它可以落在 1、2、3、4 或 6 塊瓷磚上。在六邊形網格上，它可以落在 1、2 或 3 塊瓷磚上。

這個遊戲的特殊情況給出了 布豐-拉普拉斯針問題（對於正方網格）和 布豐針問題（對於無限等距平行線）。

CleanTileSquare1
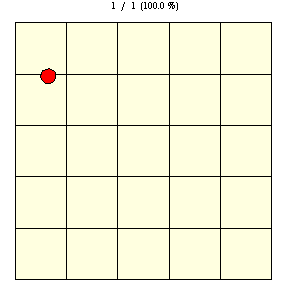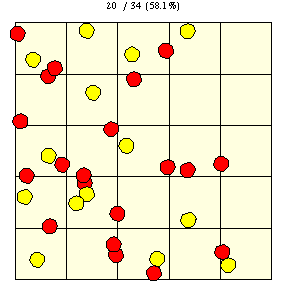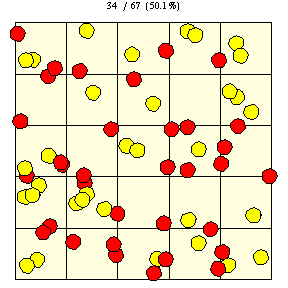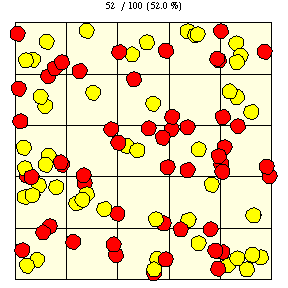
Clean tile on a square grid

如上圖所示，在瓷磚邊長為 l 的正方網格上，直徑為 d 的硬幣完全落在單塊瓷磚上的機率（圖中黃色圓盤所示）由下式給出

P_1=((l-d)^2)/(l^2)=(1-d/l)^2,
(1)

因為透過從邊長為 l 的正方形內縮硬幣半徑 d/2 而得到的正方形邊長的縮短量由下式給出

Deltal=2(1/2d)=d.
(2)

它落在兩塊或更多瓷磚上的機率（紅色圓盤所示）僅僅是

P_(>=2)=1-P_1=1-(1-d/l)^2.
(3)

為了使兩個玩家分別投注 (1) 單塊瓷磚或 (2) 兩塊或更多瓷磚的遊戲公平，這些量必須相等，由此得出

d=1/2(2-sqrt(2))l=0.29289...l.
(4)
CleanTileSquare2

落在恰好兩塊瓷磚上的機率是上圖中陰影區域與瓷磚大小的比率，即

P_2=4d/(2l)(1-d/l)
(5)
=2(1-d/l)d/l.
(6)
CleanTileSquare3

在正方網格上，硬幣落在恰好三塊瓷磚上的機率是上圖中所示區域覆蓋的瓷磚部分的比例，

P_3=(d^2-pi(1/2d)^2)/(l^2)=(1-1/4pi)(d^2)/(l^2).
(7)
CleanTileSquare4

類似地，硬幣落在四塊瓷磚上的機率是上圖中所示的圓盤覆蓋的瓷磚部分的比例，

P_4=(pi(1/2d)^2)/(l^2)=1/4pi(d^2)/(l^2).
(8)
CleanTileTriangle
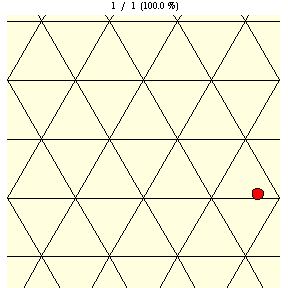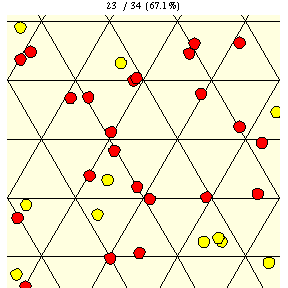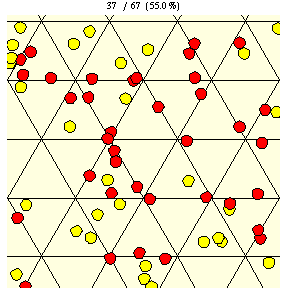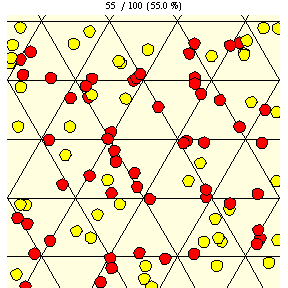
Clean tile on a triangular grid

如上圖所示，在瓷磚邊長為 l 的三角網格上，直徑為 d 的硬幣完全落在單塊瓷磚上的機率由下式給出

P_1=((l-sqrt(3)d)^2)/(l^2)=(1-sqrt(3)d/l)^2,
(9)

因為透過從邊長為 l 的等邊三角形內縮硬幣半徑 d/2 而得到的等邊三角形邊長的縮短量是

Deltal=2(1/2dcot30 degrees)=sqrt(3)d.
(10)

它落在兩塊或更多瓷磚上的機率僅僅是

P_(>=2)=1-P_1=1-(1-sqrt(3)d/l)^2.
(11)

為了使兩個玩家分別投注 (1) 單塊瓷磚或 (2) 兩塊或更多瓷磚的遊戲公平，這些量必須相等，由此得出

d=1/6(2sqrt(3)-sqrt(6))l=0.16910...l.
(12)
CleanTileHexagon

如上圖所示，在瓷磚邊長為 l 的六邊形網格上，直徑為 d 的硬幣完全落在單塊瓷磚上的機率由下式給出

P_1=((l-1/3sqrt(3)d)^2)/(l^2)=(1-1/3sqrt(3)d/l)^2,
(13)

因為透過從邊長為 l 的正六邊形內縮硬幣半徑 d/2 而得到的正六邊形邊長的縮短量是

Deltal=2(1/2d)sec30 degrees=1/3sqrt(3)d.
(14)

它落在兩塊或更多瓷磚上的機率僅僅是

P_(>=2)=1-P_1=1-(1-1/3sqrt(3)d/l)^2.
(15)

為了使兩個玩家分別投注 (1) 單塊瓷磚或 (2) 兩塊或更多瓷磚的遊戲公平，這些量必須相等，由此得出

d=1/2(2sqrt(3)-sqrt(6))l=0.50730...l.
(16)
CleanTileRhombus

在由開角為 theta 的菱形組成的四邊形平鋪中，從邊長為 l 的菱形內縮得到

Deltal_1=1/2dcottheta
(17)
Deltal_2=1/2dtantheta,
(18)

因此

Deltal=Deltal_1+Deltal_2=1/2d(cottheta+tantheta)=1/2dcscthetasectheta.
(19)

因此，硬幣落在單塊瓷磚上的機率是

P_1=((l-1/2dcscthetasectheta)^2)/(l^2)
(20)
=(1-d/(2l)cscthetasectheta)^2.
(21)

它落在兩塊或更多瓷磚上的機率僅僅是

P_(>=2)=1-P_1=1-(1-d/(2l)cscthetasectheta)^2.
(22)

為了使兩個玩家分別投注 (1) 單塊瓷磚或 (2) 兩塊或更多瓷磚的遊戲公平，這些量必須相等，由此得出

d=(2-sqrt(2))lcosthetasintheta.
(23)

正如預期的那樣，當 theta=pi/4 時，這簡化為正方形的情況。

另請參閱

布豐-拉普拉斯針問題, 布豐針問題

使用 探索

參考文獻

Buffon, G. "Essai d'arithmétique morale." Histoire naturelle, générale er particulière, Supplément 4, 46-123, 1777.Mathai, A. M. "清潔瓷磚問題 (The Clean Tile Problem)." §1.1.1 in 幾何機率導論：分佈方面及其應用 (An Introduction to Geometrical Probability: Distributional Aspects with Applications). Taylor & Francis: pp. 2-5, 1999.Solomon, H. 幾何機率 (Geometric Probability). 美國費城：SIAM, 1978.

在 中引用

清潔瓷磚問題

請引用為

Weisstein, Eric W. "清潔瓷磚問題 (Clean Tile Problem)." 來自 網路資源。 https://mathworld.tw/CleanTileProblem.html

學科分類