護城河問題

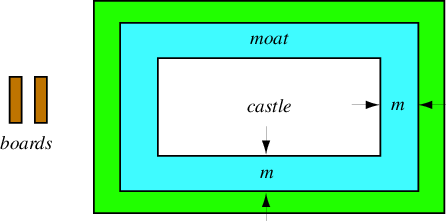
護城河問題有兩個版本，一個是幾何版本，一個是代數版本。幾何護城河問題詢問，如果 Rapunzel 只有兩塊單位長度的木板（且沒有釘子或其他方式將它們連線在一起），她可以跨越的最寬的護城河寬度是多少才能逃脫。更一般地，使用 塊木板可以跨越的最寬的護城河寬度是多少？ Matthew Cook 推測，這個問題的漸近解是 (Cook 1997)。

代數護城河問題詢問是否有可能在 實數軸 上僅使用有界長度的步長和素數上的步長走到無窮遠。答案是否定的 (Gethner et al. 1998)。然而，高斯護城河問題詢問是否有可能在 高斯整數 中使用 高斯素數 作為墊腳石並採取有界長度的步長走到無窮遠，這個問題尚未解決。Gethner et al. (1998) 表明，寬度為 的護城河是存在的。