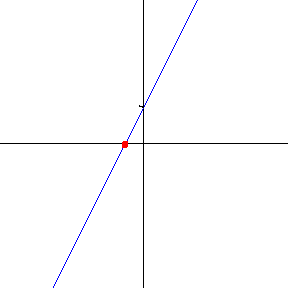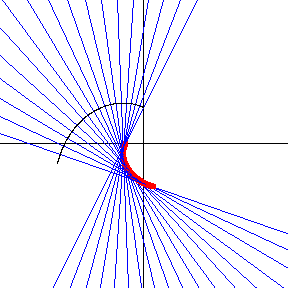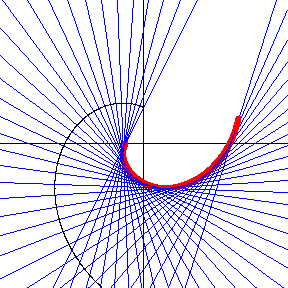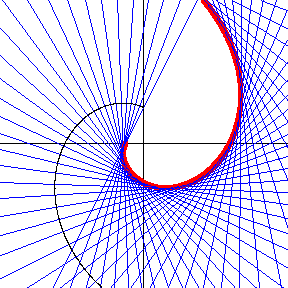
對於一個引數化表示為 對數螺線,
|
(1)
| |||
|
(2)
|
漸屈線 由下式給出
|
(3)
| |||
|
(4)
|
正如約翰·伯努利首次證明的那樣,對數螺線 的 漸屈線 因此是另一個 對數螺線,具有 和
,
在某些情況下,漸屈線 與原曲線相同,這可以透過代換新變數來證明
|
(5)
|
然後上面的方程變為
|
(6)
| |||
|
(7)
| |||
|
(8)
| |||
|
(9)
|
如果滿足以下條件,則這些方程等價於原始方程的形式
|
(10)
|
|
(11)
|
|
(12)
|
其中只有 中帶有負號的解存在。求解得到下表總結的值。
| 1 | 0.2744106319... | |
| 2 | 0.1642700512... | |
| 3 | 0.1218322508... | |
| 4 | 0.0984064967... | |
| 5 | 0.0832810611... | |
| 6 | 0.0725974881... | |
| 7 | 0.0645958183... | |
| 8 | 0.0583494073... | |
| 9 | 0.0533203211... | |
| 10 | 0.0491732529... |