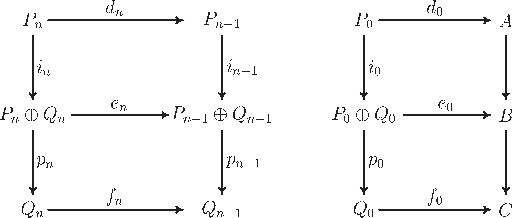
給定模的短正合序列
|
(1)
|
設
|
(2)
|
|
(3)
|
分別是 和
的投射分解。則存在
的投射分解
|
(4)
|
使得上述圖表是可交換的。這裡, 是第一個被加數的注入,而
是對於
的第二個因子的投影。
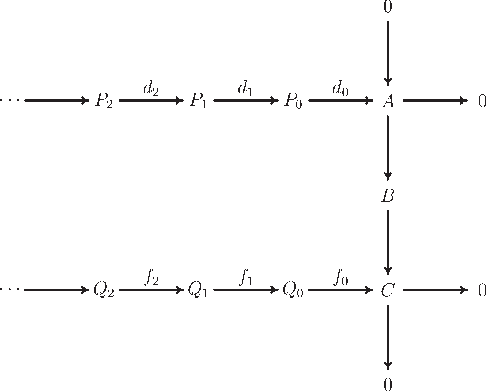
這個引理的名稱來源於短正合序列和給定的投射分解所形成的圖表的形狀。
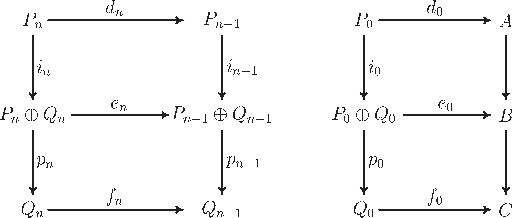
給定模的短正合序列
|
(1)
|
設
|
(2)
|
|
(3)
|
分別是 和
的投射分解。則存在
的投射分解
|
(4)
|
使得上述圖表是可交換的。這裡, 是第一個被加數的注入,而
是對於
的第二個因子的投影。

這個引理的名稱來源於短正合序列和給定的投射分解所形成的圖表的形狀。
此條目由 Margherita Barile 貢獻
Barile, Margherita. "馬蹄引理。" 來自 Web 資源,由 Eric W. Weisstein 建立。 https://mathworld.tw/HorseshoeLemma.html