平面的包絡
|
(1)
|
其中 是波在方向
(即,
、
和
是方向餘弦) 上的傳播速度,被稱為給定介質的波面(Love 1944,第 299 頁)。
在各向同性介質中, 與
、
和
無關,由下式給出
|
(2)
|
其中 是介質密度,
和
是所謂的固體的拉梅常數。然後,波面是雙葉的,兩個葉片都是球體(Love 1944,第 299 頁)。
在各向異性的情況下,曲面由三個葉片組成,對應於 的值,這些值是以下方程的根
 |
(3)
|
其中 是
、
和
的函式,以應變能函式的係數表示(Christoffel 1877,Love 1944,第 299 頁)。Green(1839)表明,對於允許純橫向平面波傳播的彈性固體的最一般情況,波面由一個球面和兩個葉片組成,這兩個葉片是平面(1)的包絡,並受以下條件約束
 |
(4)
|
其中 、
和
是曲面的特徵常數。這兩個葉片對應於所謂的菲涅耳波面(Love 1944,第 299 頁)。
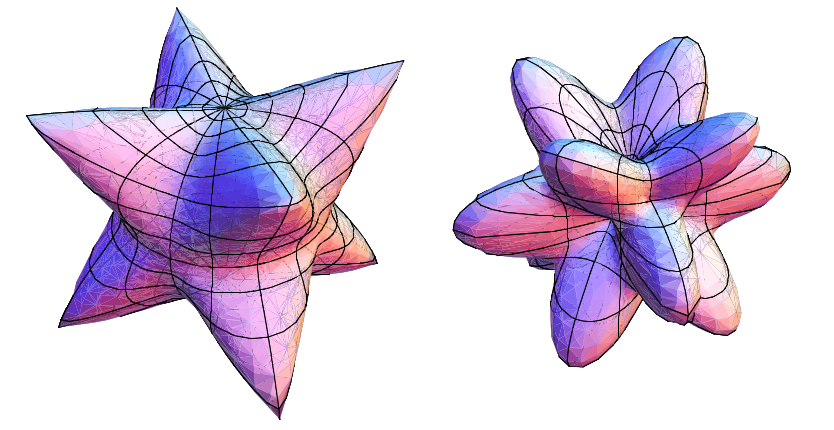
上面的影像顯示了具有特定彈性引數的菲涅耳波面的兩個葉片 (JavaView)。
von Seggern(1993,第 304 頁)將菲涅耳彈性曲面定義為由下式給出的四次曲面
|
(5)
|
其中
|
(6)
|
儘管這似乎與 Love(1944)和 JavaView 網站上描述的曲面不同。