Bootstrap 滲流

一個二維二元 () 全域細胞自動機，具有範圍為 的 馮·諾依曼鄰域。它具有一個出生規則，即其 4 個鄰居中至少有 2 個是活著的，以及一個生存規則，即所有細胞都存活。 步 Bootstrap 滲流在一個 網格上進行，初始條件為密度 的隨機初始條件，可以在 Wolfram 語言中實現為

With[{n = 10, p = 0.1, s = 20},
  CellularAutomaton[
    {1018, {2, {{0, 2, 0}, {2, 1, 2}, {0, 2, 0}}},
      {1, 1}},
    Table[If[Random[Real] < p, 1, 0],  {s},  {s}],
    n
  ]
]

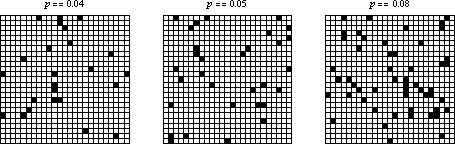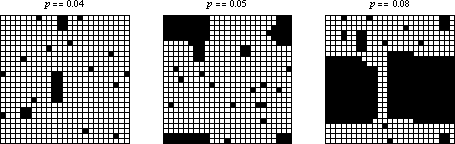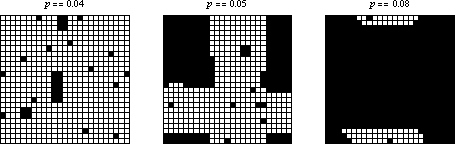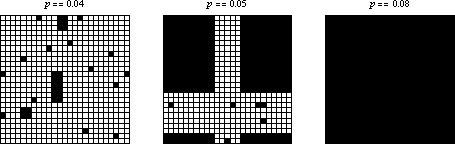
如果初始條件由密度為 的細胞的隨機稀疏排列組成，那麼系統似乎會快速收斂到由活細胞的矩形島嶼和死細胞海洋包圍的穩態。然而，當 跨越有限尺寸網格上的某個閾值時，行為似乎會發生變化，以至於每個細胞都變為活細胞。上面在三個 網格上顯示了幾個示例，這些網格具有隨機初始條件和不同的起始密度。

然而，這個結論被證明是不正確的，因為行為的明顯變化實際上是由於使用有限尺寸網格而引入的虛假邊緣效應。令人驚訝的是，Holroyd (2003) 表明漸近閾值發生，使得