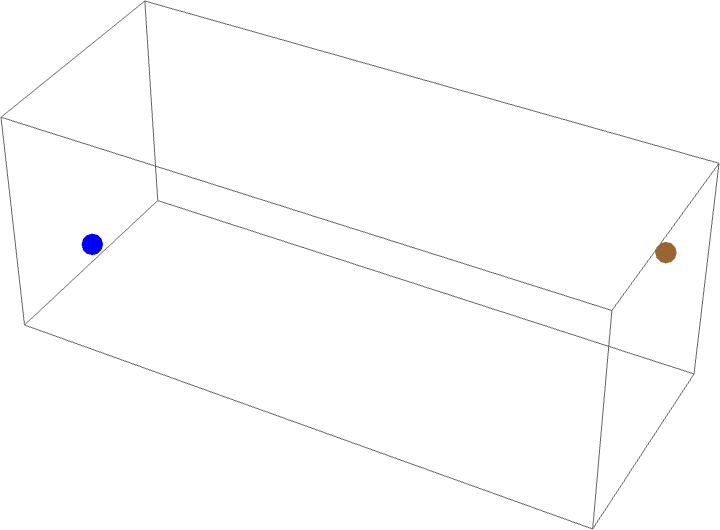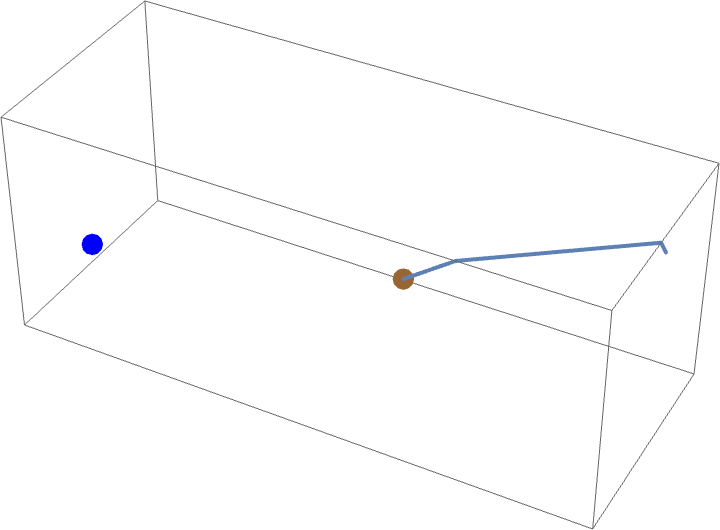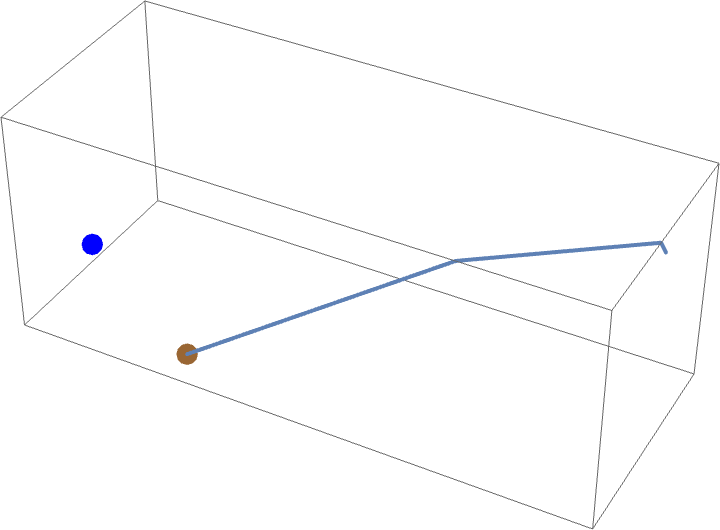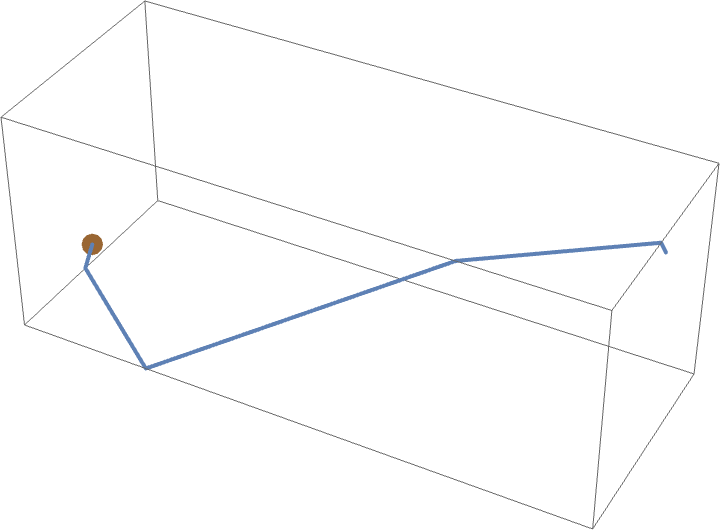
蜘蛛和蒼蠅問題考慮一個尺寸為 的長方體房間,蜘蛛位於其中一面
牆壁的中間,距離天花板一英尺。蒼蠅位於對面牆壁的中間,距離地板一英尺。如果蒼蠅保持靜止,蜘蛛為了抓住蒼蠅,沿著牆壁、天花板和地板爬行的最短總距離(即測地線)是多少?
答案 可以透過如上所示的“展開”牆壁獲得。請注意,這個距離比蜘蛛必須先沿著牆壁爬到地板,然後穿過地板,再向上爬一英尺才能到達蒼蠅的
短。這個謎題最初由杜德尼於 1903 年在英國一家報紙上提出(Gardner 1958)。
這個問題的一個變體是,蜘蛛可以用蛛絲把自己懸掛起來,從而抄近路,而不必被迫粘在房間的表面上。如果蜘蛛在他的起始位置將一根蛛絲附著在牆上,然後把自己放到地板上(因此不爬行一英寸),那麼他就可以步行穿過房間的長度 (),再向上爬一英尺,從而在總共爬行
後到達他的獵物(雖然總距離當然是
)。
如果蜘蛛不擅長將蛛絲固定在垂直牆壁上,他仍然可以透過僅爬行 來抓住蒼蠅。特別是,他可以爬到天花板 (
),然後橫穿天花板的長度 (
),再降低
(無需爬行),從而抓住蒼蠅。