主題
Search

Borel-Tanner 分佈

BorelTannerDistribution

設 S_n 為 {1, 2, ..., n} 的置換集合，並設 sigma_t 為 S_n 上的連續時間隨機遊走，它是以速率 1 執行隨機選擇的換位操作的結果。設 d(sigma_t) 為在時間 t 從單位元 I 的距離，即返回到 I 所需的最少換位數。然後當 n->infty 時，d(sigma_(nc/2))/n->u(c)，其中

u(c)=1-sum_(k=1)^infty(k^(k-2))/(ck!)(ce^(-c))^k

（Berestycki 2004；Berestycki 和 Durrett 2004），其中 u(c) 被稱為 Borel-Tanner 分佈 (Trott 2006, p. 284)。

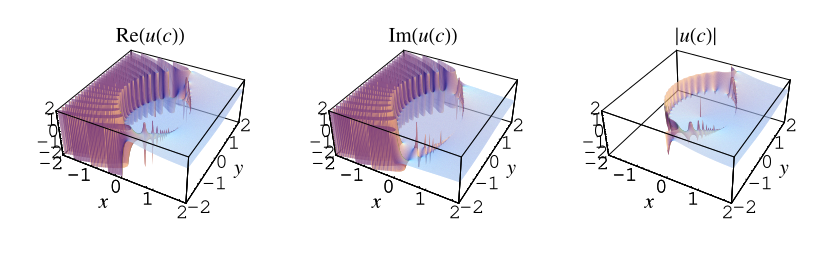
BorelTannerDistributionReIm

複數 c 的 Borel-Tanner 分佈在複平面上方的圖中繪製 (Trott 2006, p. 284)。

有趣的是，對於 0<=c<=1，此函式的值為 c/2 (Berestycki 2004；Trott 2006, p. 284)。

使用 探索

參考文獻

Berestycki, N. “隨機轉置的雙曲幾何。” 2004年10月31日。 http://arxiv.org/abs/math.PR/0411011。Berestycki, N. 和 Durrett, R. “隨機轉置隨機遊走中的相變。” Probab. Theor. Rel. Fields 136, 203-233, 2006年。Haight, F. A. 和 Breuer, M. A. “Borel-Tanner 分佈。” Biometrika 47, 143-150, 1960。Trott, M. The Mathematica GuideBook for Numerics. 紐約：Springer-Verlag，2006年。 http://www.mathematicaguidebooks.org/。

在 中引用

Borel-Tanner 分佈

請按如下方式引用

Weisstein, Eric W. “Borel-Tanner 分佈。” 來自 —— 資源。 https://mathworld.tw/Borel-TannerDistribution.html

學科分類